por Francisco Javier Rodríguez Arias

Este 14 de junio comienza la Copa Mundial de la FIFA Rusia 2018 (Чемпионат мира по футболу Россия 2018). Después de leer la predicción de El País (véase [1] y [2]), me pregunté si podría hacer mi propia simulación usando Wolfram Language. Entonces, aquí está mi intento. Toda idea para mejorarlo es bienvenida, ¡y que gane el mejor!

Introducción

Construiré esta simulación por bloques:

1. Información básica
2. Simulación de un juego
3. Simulación de la fase de grupos
4. Simulación de la segunda fase
5. Juntando todo

1. Información básica

1.1. Clasificación

Como base para este modelo usaré la clasificación mundial de la FIFA. Podríamos probar también otras clasificaciones, como el creado por El País.

En primer lugar, he bajado el ranking de la FIFA, y usé Interpreter["Country"] sobre todos los nombres, y pude obtener las entidades de los países para casi todos los casos. Como sabemos, el Reino Unido no juega unido en el fútbol, así que tuve que utilizar Interpreter["AdministrativeDivision"] para las naciones constitutivas del Reino Unido. Otros casos también tuvieron problemas y tuve que hacer un alineamiento manual, como el caso de Tahití o de Congo (donde es ambiguo a cuál se refiere). Adjunto aquí el resultado de esa clasificación, así que en esta simulación simplemente podemos cargarlo:

rankingPoints = Dispatch[Get["rankingFifaJune7.m"]]

1.2. Participantes y grupos

Usando la clasificación anterior, tomé la lista de participantes de la página de la FIFA y la convertí en una simple lista de países:

countries = {Entity["Country", "Russia"], 
  Entity["Country", "SaudiArabia"], Entity["Country", "Egypt"], 
  Entity["Country", "Uruguay"], Entity["Country", "Portugal"], 
  Entity["Country", "Spain"], Entity["Country", "Morocco"], 
  Entity["Country", "Iran"], Entity["Country", "France"], 
  Entity["Country", "Australia"], Entity["Country", "Peru"], 
  Entity["Country", "Denmark"], Entity["Country", "Argentina"], 
  Entity["Country", "Iceland"], Entity["Country", "Croatia"], 
  Entity["Country", "Nigeria"], Entity["Country", "Brazil"], 
  Entity["Country", "Switzerland"], Entity["Country", "CostaRica"], 
  Entity["Country", "Serbia"], Entity["Country", "Germany"], 
  Entity["Country", "Mexico"], Entity["Country", "Sweden"], 
  Entity["Country", "SouthKorea"], Entity["Country", "Belgium"], 
  Entity["Country", "Panama"], Entity["Country", "Tunisia"], 
  Entity["AdministrativeDivision", {"England", "UnitedKingdom"}], 
  Entity["Country", "Poland"], Entity["Country", "Senegal"], 
  Entity["Country", "Colombia"], Entity["Country", "Japan"]}

 

Dado que está ordenado por grupos, podemos usar Partition para obtener los equipos por grupo:

teamsByGroup = AssociationThread[CharacterRange["A", "H"] -> Partition[countries, 4]]

 

2. Simulación de un juego

Esta es probablemente la parte más difícil de este problema. ¿Cómo predecir el resultado de un partido? Si fuera fácil, ¡ni se jugaría! Bueno, usaré el mismo sistema de predicción empleado en otras fuentes (como en este artículo), el cual se basa en una distribución de Poisson usando la razón entre las clasificaciones de la FIFA. Agrego también otro factor que podría servir para ajustar el resultado aumentando la probabilidad de un equipo (por ejemplo, Rusia puede no tener un buen lugar en la clasificación, pero está jugando en casa, y eso podría considerarse como algo a su favor).

Cuando no se permite empate, en vez de hacer solo un tiempo extra y una ronda de penales, simplemente ejecutaré la rutina básica de resultados hasta que no haya empate. Para obtener un resultado más exacto podríamos ejecutar solo una vez más la distribución base (por el tiempo extra) y luego usar una distribución binomial para los penales.

getPossibleResult[weight1_, weight2_, lambda1_, lambda2_] := 
    {RandomVariate[PoissonDistribution[lambda1 weight1/weight2]], RandomVariate[PoissonDistribution[lambda2 weight2/weight1]]};

simulateMatch[weight1_, weight2_, lambda1_, lambda2_, drawQ_] := Module[{result}, 
    result = getPossibleResult[weight1, weight2, lambda1, lambda2];
    If[!drawQ,
        While[SameQ @@ result,
            result = getPossibleResult[weight1, weight2, lambda1, lambda2]
        ];
    ];
    result
];

simulatedMatchResults[match["Groups"][team1_, team2_]] := simulateMatch[team1 /. rankingPoints, team2 /. rankingPoints, 1, 1, True];
simulatedMatchResults[match["Knockout"][team1_, team2_]] := simulateMatch[team1 /. rankingPoints, team2 /. rankingPoints, 1, 1, False];

 

En este modelo usaré un lambda de 1, pero podríamos generar otra lista de valores para modificar, por ejemplo, el peso de Rusia al ser dueño de casa, o agregar más fortaleza a nuestro equipo favorito. Por supuesto, cualquier cambio radical en los valores cambiaría totalmente los resultados, así que no recomendaría usarlos para hacer apuestas.

3. Simulación de la fase de grupos

Para simular cada grupo, jugaremos cada partido y, luego, calcularemos la tabla completa de resultados ordenada por puntos, diferencia de goles, goles a favor y goles en contra.

simulateGroup[groupsTeam_] := 
Module[{matches = DeleteDuplicatesBy[Permutations[groupsTeam, {2}], Sort], matchResults, resultsTable, resultsLookup},
    resultsLookup[_, _] = 0;
    matchResults = {##, simulatedMatchResults[match["Groups"][##]]} & @@@ matches;
    Function[{team1, team2, result},
        Switch[result,
            {a_, b_} /; a > b,
                resultsLookup[team1, "WINS"] = resultsLookup[team1, "WINS"] + 1;
                resultsLookup[team2, "LOSTS"] = resultsLookup[team2, "LOSTS"] + 1;
                resultsLookup[team1, "POINTS"] = resultsLookup[team1, "POINTS"] + 3;
            ,
            {a_, b_} /; a < b,
                resultsLookup[team2, "WINS"] = resultsLookup[team2, "WINS"] + 1;
                resultsLookup[team1, "LOSTS"] = resultsLookup[team1, "LOSTS"] + 1;
                resultsLookup[team2, "POINTS"] = resultsLookup[team2, "POINTS"] + 3;
            ,
            _
            ,
                resultsLookup[team1, "DRAWS"] = resultsLookup[team1, "DRAWS"] + 1;
                resultsLookup[team2, "DRAWS"] = resultsLookup[team2, "DRAWS"] + 1;
                resultsLookup[team1, "POINTS"] = resultsLookup[team1, "POINTS"] + 1;
                resultsLookup[team2, "POINTS"] =  resultsLookup[team2, "POINTS"] + 1;
        ];
        resultsLookup[team1, "GOL+"] = resultsLookup[team1, "GOL+"] + result[[1]];
        resultsLookup[team2, "GOL+"] = resultsLookup[team2, "GOL+"] + result[[2]];
        resultsLookup[team1, "GOL-"] = resultsLookup[team1, "GOL-"] + result[[2]];
        resultsLookup[team2, "GOL-"] = resultsLookup[team2, "GOL-"] + result[[1]];
    ] @@@ matchResults;
    resultsTable = Table[
        {
            t,
            resultsLookup[t, "POINTS"],
            resultsLookup[t, "WINS"],
            resultsLookup[t, "LOSTS"],
            resultsLookup[t, "DRAWS"],
            resultsLookup[t, "GOL+"],
            resultsLookup[t, "GOL-"],
            resultsLookup[t, "GOL+"] - resultsLookup[t, "GOL-"]
        }, {t, groupsTeam}];
    SortBy[resultsTable, {-#[[2]], -#[[-1]], -#[[-3]], #[[-2]]} &]
];

selectClassified[groupResultTable_] := groupResultTable[[;;2, 1]];

simulateAllGroups[groups_] := simulateGroup /@ groups;

selectAllClassified[groupsResults_] := AssociationMap[List["1"<>#[[1]]->#[[2, 1]],"2"<>#[[1]]->#[[2, 2]]] &, selectClassified /@ groupsResults]

 

4. Simulación de la segunda fase

4.1. Cronograma de juegos

El primer paso aquí es conseguir la lista de partidos. ¿Quién juega contra quién en cada ronda eliminatoria? Eso lo sacamos de la página de la FIFA, y para guardarlo usaré una lista de reglas de la forma matchnumber -> {team1, team2}, donde team1 y team2 serán cadenas de caracteres de la forma "1"|"2" ~~ group o "W"|"L" ~~ matchnumber.

roundOf16 = Thread[Range[49, 56] -> {{"1C", "2D"}, {"1A", "2B"}, {"1B", "2A"}, {"1D", "2C"}, {"1E", "2F"}, {"1G", "2H"}, {"1F", "2E"}, {"1H", "2G"}}];

quarters = Thread[Range[57, 60] -> {{"W49", "W50"}, {"W53", "W54"}, {"W55", "W56"}, {"W51", "W52"}}];

semifinals = {61 -> {"W57", "W58"}, 62 -> {"W59", "W60"}};

thirdplace = {63 -> {"L61", "L62"}};

final = {64 -> {"W61", "W62"}}

 

Con todo esto podemos definir la competición como una grupo de rondas sucesivas:

competition = {roundOf16, quarters, semifinals, Join[thirdplace, final]};

 

4.2. Jugando la fase

Jugar una ronda significa hacer los partidos y devolver los resultados, y para hacerlo más fácil, los resultados se acumularán, así que podemos usar Fold para tener los resultados completos.

playRound[round_, previousWL_] := Join[
    previousWL,
    Association@Flatten@Map[
        Thread[
            {"L" <> ToString[#[[1]]], "W" <> ToString[#[[1]]]} -> 
            #[[2]][[Ordering[simulatedMatchResults[match["Knockout"] @@ #[[2]]]]]]
        ] &,
        round /. previousWL
    ]
];

playRounds[groupsResults_] := Fold[playRound[#2, #1] &, groupsResults, competition]

 

4.3. Primeras estadísticas

Con todos los resultados, la primera estadística que se me ocurrió fue en cuál posición cada equipo termina. Solo me fijé en los equipos que pasaban a la segunda fase. Claro que ejecutando estas simulaciones suficientes veces, todos los equipos en algún momento pasarán a la segunda fase, eso espero.

Primero definamos una función que nos devuelva la posición de cada equipo dependiendo de cuál partido perdieron (o ganaron, para el caso del tercer y primer lugar):

posByLost = Flatten[Thread /@ {
    ("L" <> ToString[#] & /@ roundOf16[[All, 1]]) -> 9,
    ("L" <> ToString[#] & /@ quarters[[All, 1]]) -> 5,
    "L63" -> 4, "W63" -> 3, "L64" -> 2, "W64" -> 1, _ -> None
}]

(posByLostFun[#1] = #2) & @@@ posByLost;

 

Si aplicamos esa función al resultado de playRounds podemos obtener qué posición cada equipo consiguió:

getPosition[globalResults_] := Reverse[Sort[DeleteCases[KeyValueMap[posByLostFun[#1] -> #2 &, globalResults], None -> _]], {2}]

 

I si tenemos múltiples resultados de getPosition podríamos hacer un resumen:

summaryPositions[positions_] := SortBy[
    With[{n = Length[positions]},
        GroupBy[Join @@ positions, First -> Last, Sort[(#1 -> N[#2/n] & @@@ Tally[#])] &]
    ],
    -Accumulate[Lookup[#, {1, 2, 3, 4, 5, 9}, 0]] &
];

 

Pero dado que es más común hablar del ganador, finalista, semifinalista, etc, hagamos una función para calcular exactamente eso, usando como entrada el resultado anterior:

accumulatePositions[pos_] := Association@
    ReleaseHold[
        {
            "Ganador" -> Hold[1],
            "Finalista" -> Hold[1] + Hold[2], 
            "Semifinalista" -> Hold[1] + Hold[2] + Hold[3] + Hold[4], 
            "Cuartos" -> Hold[1] + Hold[2] + Hold[3] + Hold[4] + Hold[5], 
            "Octavos" -> Hold[1] + Hold[2] + Hold[3] + Hold[4] + Hold[5] + Hold[9]
        } /. Append[pos, _Integer -> 0]
    ];

 

4.4. Otras ideas de más estadísticas

Otras estadísticas se puede hacer también con estas funciones, como por ejemplo, calcular cuál sería la final más probable, o contra cuáles equipos tu equipo favorito jugará.

5. Juntando todo

Ya tenemos todas las herramientas necesarias para ejecutar una copa del mundo n veces:

simulateWC[n_] := accumulatedPositions[
    summaryPositions[
        Table[
            getPosition[
                playRounds[
                    selectAllClassified[
                        simulateAllGroups[
                            teamsByGroup
                        ]
                    ]
                ]
            ],
            n
        ]
    ]
];

 

Y podemos definir una función para mostrarlo:

displaySimulationResult[sr_] := (Dataset`$DatasetTargetRowCount = 40; Dataset[sr /. x_?NumericQ :> Quantity[100 x, "Percent"]])

 

(Ya sé que siempre digo que Dataset es para mucho más que simplemente mostrar tablas, pero es que se ven muy bien).

5.1. Usando la simulación

Ahora ya podemos jugar con nuestras funciones y hacer miles de simulaciones, 100000 o más si tienes memoria y tiempo. Y obtener así las probabilidades simplemente contando.

Algunos resultados:

simulation100k = simulateWC[100000];

 

Y podemos mostrarlos:

displaySimulationResult[simulation100k]

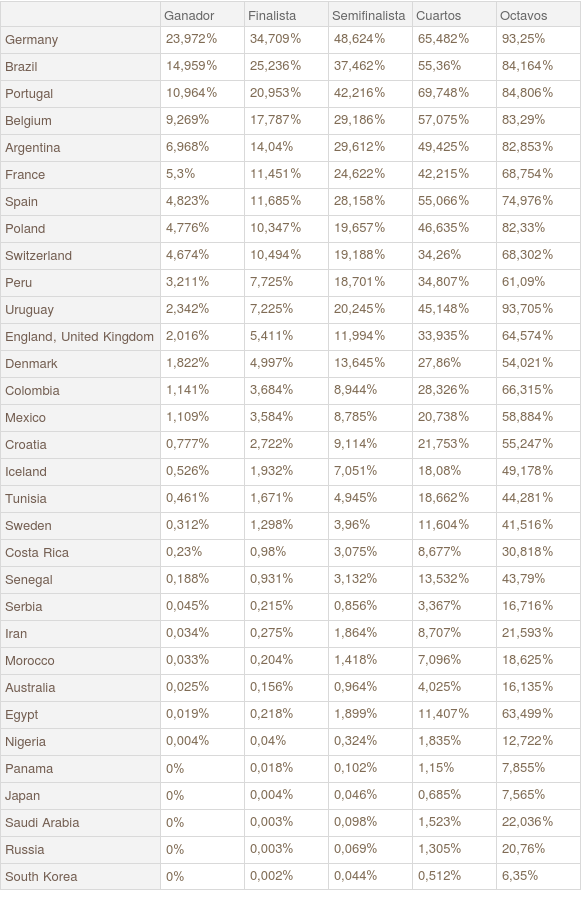
5.1.1. Agregando mapas

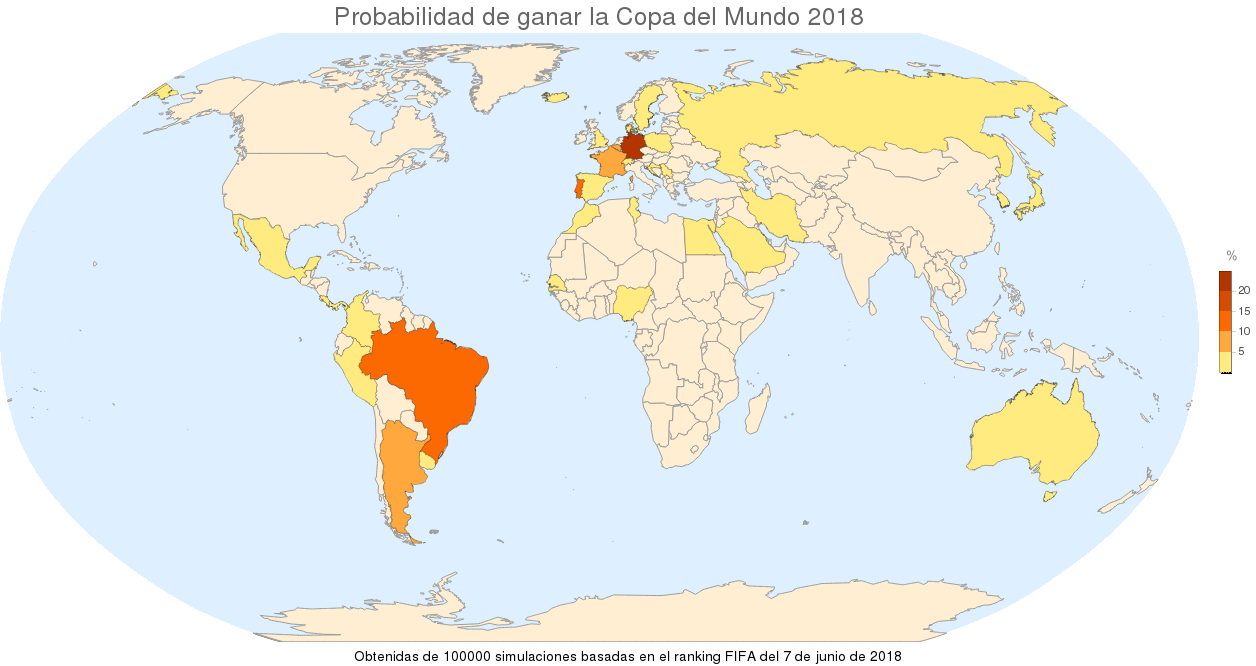
Podemos hacer un mapa de las probabilidades de ganar y de pasar a la segunda fase:

Labeled[GeoRegionValuePlot[Quantity[100 #["Winner"], "Percent"] & /@ simulation100k, 
    GeoBackground -> "CountryBorders", GeoProjection -> "Robinson", ImageSize -> 1200, 
    PlotLabel -> Style["Probabilidad de ganar la Copa del Mundo 2018", 24]],
    Text["Obtenidas de 100000 simulaciones basadas en el ranking FIFA del 7 de junio de 2018"]
]

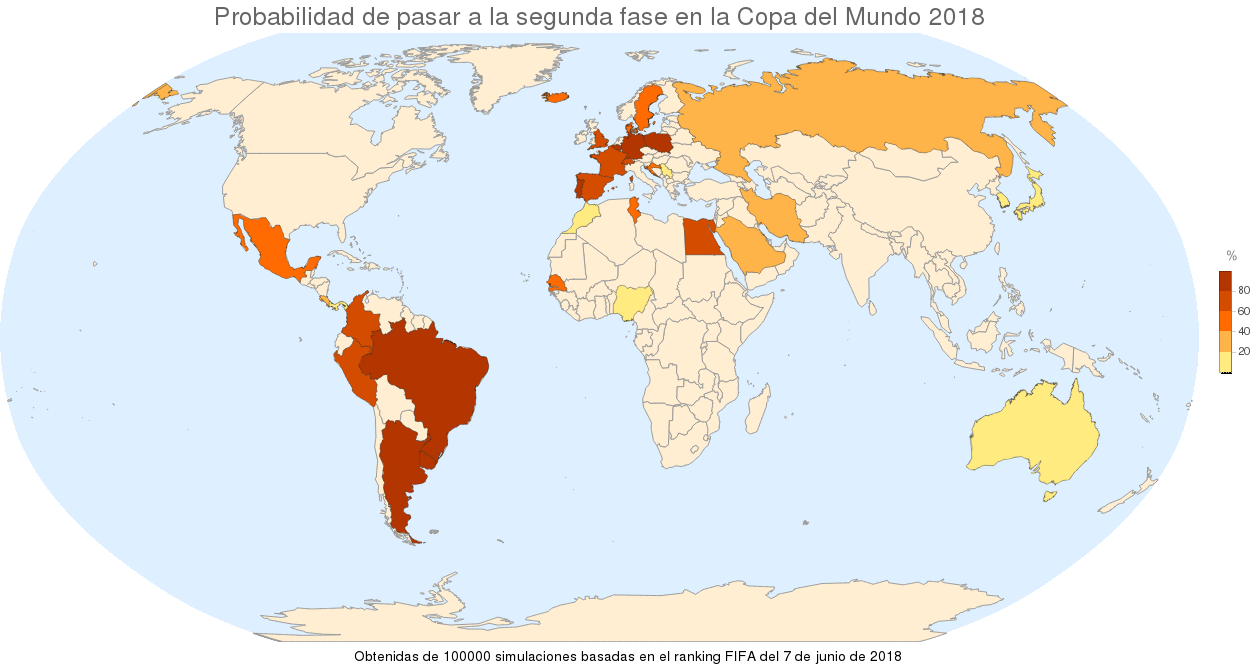
Labeled[GeoRegionValuePlot[Quantity[100 #["Round16"], "Percent"] & /@ simulation100k, 
    GeoBackground -> "CountryBorders", GeoProjection -> "Robinson", ImageSize -> 1200, 
    PlotLabel -> Style["Probabilidad de pasar a la segunda fase en la Copa del Mundo 2018", 24]], 
    Text["Obtenidas de 100000 simulaciones basadas en el ranking FIFA del 7 de junio de 2018"]
]

5.2. Final deseado

¿Podemos calcular la probabilidad de ver nuestro final favorito? No es difícil usando las funciones desarrolladas aquí, simplemente significaría calcular la probabilidad que los dos equipos que quieres lleguen a la final en forma simultánea. Digamos que queremos ver un Perú – Brasil, y claro, con la espectativa que gane Perú :).

Usaré esta vez 10000 simulaciones:

Block[{n = 10000, c = 0},
    Do[
        c += Boole[MatchQ[Sort[{"W64", "L64"} /. playRounds[selectAllClassified[simulateAllGroups[teamsByGroup]]]], {Entity["Country", "Brazil"], Entity["Country", "Peru"]}]];
        , n
    ];
    Quantity[100.0 c/n, "Percent"]
]

 

Y luego de hacerlo obtenemos 0,85%, no tan bueno como quisiéramos.

Conclusiones

1. ¡Esto será divertido!
2. Esta simulación se basa en un ranking dado, pero es fácil de cambiar eso, y obtener resultados de acuerdo a diferentes factores o expectativas.
3. Como tarea pendiente queda el agregar un factor extra para cada equipo (o par de equipos)

Nota: este artículo fue publicado también en Wolfram Community: 2018 FIFA World Cup Russia Simulation